CHAPTER 1
Neural Networks
Introduction
An artificial neural network (sometimes abbreviated ANN, or shortened to just "neural network" when the context is clear) is a software system that loosely models biological neurons and synapses. Before explaining exactly how neural networks work, it is useful to understand what types of problems they can solve. The image in Figure 1-a represents a typical problem that might be solved using a neural network.

Figure 1-a: A Typical Problem
The goal of the problem is to predict a person's political inclination based on his or her gender, age, home location, and annual income. One hurdle for those new to neural networks is that the vocabulary varies greatly. The variables used to make a prediction can be called independent variables, predictors, attributes, features, or x-values. The variable to predict can be called the dependent variable, the y-value, or several other terms.
The type of problem shown in Figure 1-a is called a classification problem because the y-value can take one of three possible class values: conservative, liberal, or moderate. It would be perfectly possible to predict any of the other four variables. For example, the data could be used to predict a person's income based on his or her gender, age, home location, and political inclination. Problems like this, where the y-value is numeric, are often called regression problems.
There are many other related problem scenarios that are similar to the one shown in Figure 1-a. For example, you could have several million x-values where each represents the pixel value in a photograph of a person, and a y-value that represents the class of the picture, such as "on security watch list" or "not on watch list". Such problems are sometimes called image recognition problems. Or imagine x-values that represent digitized audio signals and y-values that represent vocabulary words such as "hello" and "quit". This is speech recognition.
Neural networks are not magic and require data with known y-values, called the training data. In Figure 1-a there are only four training items. In a realistic scenario you would likely have hundreds or thousands of training items.
The diagram in Figure 1-b represents a neural network that predicts the political inclination of a male who is 35 years old, lives in a rural area, and has an annual income of $49,000.00.

Figure 1-b: A Neural Network
As you will see shortly, a neural network is essentially a complicated mathematical function that understands only numbers. So, the first step when working with a neural network is to encode non-numeric x-data, such as gender and home location, into numeric data. In Figure 1-b, "male" is encoded as -1.0 and "rural" is encoded as (1.0, 0.0).
In addition to encoding non-numeric x-data, in many problems numeric x-data is normalized so that the magnitudes of the values are all roughly in the same range. In Figure 1-b, the age value of 35 is normalized to 3.5 and the income value of $49,000.00 is normalized to 4.9. The idea is that without normalization, x-variables that have values with very large magnitudes can dominate x-variables that have values with small magnitudes.
The heart of a neural network is represented by the central box. A typical neural network has three levels of nodes. The input nodes hold the x-values. The hidden nodes and output nodes perform processing. In Figure 1-b, the output values are (0.23, 0.15, 0.62). These three values loosely represent the probability of conservative, liberal, and moderate respectively. Because the y-value associated with moderate is the highest, the neural network concludes that the 35-year-old male has a political inclination that is moderate.
The dummy neural network in Figure 1-b has 5 input nodes, 4 hidden nodes, and 3 output nodes. The number of input and output nodes are determined by the structure of the problem data. But the number of hidden nodes can vary and is typically found through trial and error. Notice the neural network has (5 * 4) + (4 * 3) = 32 lines connecting the nodes. Each of these lines represents a numeric value, for example -1.053 or 3.987, called a weight. Also, each hidden and output node (but not the input nodes) has an additional special kind of weight, shown as a red line in the diagram. These special weights are called biases.
A neural network's output values are determined by the values of the inputs and the values of the weights and biases. So, the real question when using a neural network to make predictions is how to determine the values of the weights and biases. This process is called training.
Put another way, training a neural network involves finding a set of values for the weights and biases so that when presented with training data, the computed outputs closely match the known, desired output values. Once the network has been trained, new data with unknown y-values can be presented and a prediction can be made.
This book will show you how to create neural network systems from scratch using the C# programming language. There are existing neural network applications you can use, so why bother creating your own? There are at least four reasons. First, creating your own neural network gives you complete control over the system and allows you to customize the system to meet specific problems. Second, if you learn how to create a neural network from scratch, you gain a full understanding of how neural networks work, which allows you to use existing neural network applications more effectively. Third, many of the programming techniques you learn when creating neural networks can be used in other programming scenarios. And fourth, you might just find creating neural networks interesting and entertaining.
Data Encoding and Normalization
One of the essential keys to working with neural networks is understanding data encoding and normalization. Take a look at the screenshot of a demo program in Figure 1-c. The demo program begins by setting up four hypothetical training data items with x-values for people's gender, age, home location, and annual income, and y-values for political inclination (conservative, liberal, or moderate). The first line of dummy data is:
Male 25 Rural 63,000.00 Conservative
The demo performs encoding on the non-numeric data (gender, locale, and politics). There are two kinds of encoding used, effects encoding for non-numeric x-values and dummy encoding for non-numeric y-values. The first line of the resulting encoded data is:
-1 25 1 0 63,000.00 1 0 0
After all data has been converted to numeric values, the data is stored into a matrix in memory and displayed. Next, the demo performs normalization on the numeric x-values (age and income). The first line of encoded and normalized data is:
-1.00 -0.84 1.00 0.00 0.76 1.00 0.00 0.00
The demo uses two different types of normalization, Gaussian normalization on the age values, and min-max normalization on the income values. Values that are Gaussian normalized take on values that are typically between -10.0 and +10.0. Values that are min-max normalized usually take on values that are between 0.0 and 1.0, or between -1.0 and +1.0.
The demo program uses two different types of normalization just to illustrate the two techniques. In most realistic situations you would use either Gaussian or min-max normalization for a problem, but not both. As a general rule of thumb, min-max normalization is more common than Gaussian normalization.
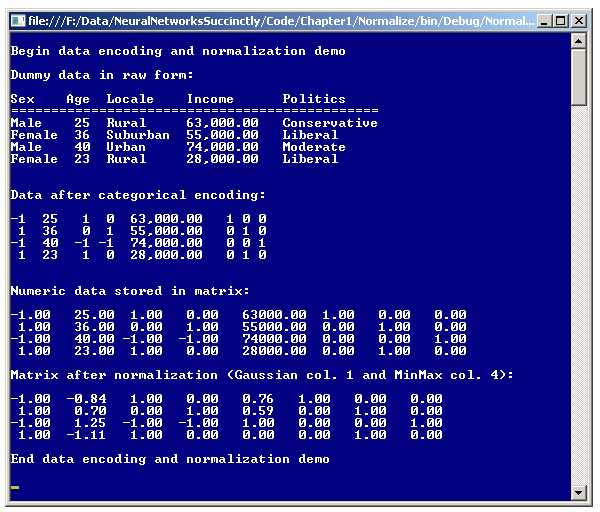
Figure 1-c: Data Encoding and Normalization
Overall Demo Program Structure
To create the demo program, I opened Visual Studio, selected the C# console application project template, and named it Normalize. The demo program has no significant .NET version dependencies, so any version of Visual Studio should work. After the template code loaded in the editor, in the Solution Explorer window I renamed the Program.cs file to the slightly more descriptive NormalizeProgram.cs, and Visual Studio automatically renamed the Program class.
At the top of the source code I deleted all using statements except the one that references the top-level System namespace. The demo was written using a static-method approach rather than an object-oriented approach for simplicity and ease of refactoring.
The overall structure of the demo program is presented in Listing 1-a. Methods GaussNormal and MinMaxNormal operate on a matrix of numeric values and normalize a single column of the matrix. Methods ShowMatrix and ShowData are just convenience helpers to keep the Main method a bit tidier. Method EncodeFile operates on a text file and performs either effects encoding or dummy encoding on a specified column of the file.
Methods EffectsEncoding and DummyEncoding are helpers that are called by the method EncodeFile. The demo program has all normal error-checking code removed in order to keep the main ideas as clear as possible.
using System;
namespace Normalize
{
class NormalizeProgram
{
static void Main(string[] args)
{
Console.WriteLine("\nBegin data encoding and normalization demo\n");
// Set up raw source data.
// Encode and display data.
// Normalize and display data.
Console.WriteLine("\nEnd data encoding and normalization demo\n");
Console.ReadLine();
}
static void GaussNormal(double[][] data, int column) { . . }
static void MinMaxNormal(double[][] data, int column) { . . }
static void ShowMatrix(double[][] matrix, int decimals) { . . }
static void ShowData(string[] rawData) { . . }
static void EncodeFile(string originalFile, string encodedFile,
int column, string encodingType) { . . }
static string EffectsEncoding(int index, int N) { . . }
static string DummyEncoding(int index, int N) { . . }
} // Program class
} // ns
Listing 1-a: Encoding and Normalization Demo Program Structure
All program control logic is contained in method Main. The method definition begins:
static void Main(string[] args)
{
Console.WriteLine("\nBegin data encoding and normalization demo\n");
string[] sourceData = new string[] {
"Sex Age Locale Income Politics",
"==============================================",
"Male 25 Rural 63,000.00 Conservative",
"Female 36 Suburban 55,000.00 Liberal",
"Male 40 Urban 74,000.00 Moderate",
"Female 23 Rural 28,000.00 Liberal" };
Four lines of dummy data are assigned to an array of strings named sourceData. The items in each string are artificially separated by multiple spaces for readability. Next, the demo displays the dummy source data by calling helper method ShowData:
Console.WriteLine("Dummy data in raw form:\n");
ShowData(sourceData);
The helper display method is defined:
static void ShowData(string[] rawData)
{
for (int i = 0; i < rawData.Length; ++i)
Console.WriteLine(rawData[i]);
Console.WriteLine("");
}
Next, the demo program manually sets up and displays an encoded version of the dummy source data:
string[] encodedData = new string[] {
"-1 25 1 0 63,000.00 1 0 0",
" 1 36 0 1 55,000.00 0 1 0",
"-1 40 -1 -1 74,000.00 0 0 1",
" 1 23 1 0 28,000.00 0 1 0" };
Console.WriteLine("\nData after categorical encoding:\n");
ShowData(encodedData);
Again, the items are artificially separated by multiple spaces. Because there are only four lines of training data, the data was manually encoded. In most situations, training data will be in a text file and will not be manually encoded, but will be encoded in one of two ways. The first approach to encoding training data in a text file is to use the copy and paste feature in a text editor such as Notepad. This is generally feasible with relatively small files (say, fewer than 500 lines) that have relatively few categorical values (about 10 or less).
The second approach is to programmatically encode data in a text file. Exactly how to encode non-numeric data and how to programmatically encode data stored in a text file will be explained shortly.
After all non-numeric data has been encoded to numeric values, the dummy data is manually stored into a matrix and displayed:
Console.WriteLine("\nNumeric data stored in matrix:\n");
double[][] numericData = new double[4][];
numericData[0] = new double[] { -1, 25.0, 1, 0, 63000.00, 1, 0, 0 };
numericData[1] = new double[] { 1, 36.0, 0, 1, 55000.00, 0, 1, 0 };
numericData[2] = new double[] { -1, 40.0, -1, -1, 74000.00, 0, 0, 1 };
numericData[3] = new double[] { 1, 23.0, 1, 0, 28000.00, 0, 1, 0 };
ShowMatrix(numericData, 2);
In most situations, your encoded data will be in a text file and programmatically loaded into a matrix along the lines of:
double[][] numericData = LoadData("..\\EncodedDataFile");
Example code to load a matrix from a text file is presented and fully explained in Chapter 5. Helper method ShowMatrix is defined:
static void ShowMatrix(double[][] matrix, int decimals)
{
for (int i = 0; i < matrix.Length; ++i)
{
for (int j = 0; j < matrix[i].Length; ++j)
{
double v = Math.Abs(matrix[i][j]);
if (matrix[i][j] >= 0.0)
Console.Write(" ");
else
Console.Write("-");
Console.Write(v.ToString("F" + decimals).PadRight(5) + " ");
}
Console.WriteLine("");
}
}
Neural network systems make extensive use of matrices. Even if you are an experienced programmer, unless you have done numerical or scientific programming, you may not be very familiar with working with matrices. Here, a matrix is defined as an array of arrays. Unlike many programming languages, C# supports a true multidimensional-array style matrix. For example:
double[,] matrix = new double[3,2]; // 3 rows and 2 cols.
However, for neural network systems, array-of-arrays style matrices are more convenient to work with because each row can be referenced as a separate array.
The Main method concludes by programmatically normalizing the age and income columns (columns 1 and 4) of the data matrix:
GaussNormal(numericData, 1);
MinMaxNormal(numericData, 4);
Console.WriteLine("\nMatrix after normalization (Gaussian col. 1" +
" and MinMax col. 4):\n");
ShowMatrix(numericData, 2);
Console.WriteLine("\nEnd data encoding and normalization demo\n");
Console.ReadLine();
} // Main
In most situations, numeric x-data will be normalized using either Gaussian or min-max but not both. However, there are realistic scenarios where both types of normalization are used on a data set.
Effects Encoding and Dummy Encoding
Encoding non-numeric y-data to numeric values is usually done using a technique called 1-of-N dummy encoding. In the demo, the y-variable to predict can take one of three values: conservative, liberal, or moderate. To encode N non-numeric values, you use N numeric variables like so:
conservative -> 1 0 0
liberal -> 0 1 0
moderate -> 0 0 1
You can think of each of the three values representing the amount of "conservative-ness", "liberal-ness", and "moderate-ness" respectively.
The ordering of the dummy encoding associations is arbitrary, but if you imagine each item has an index (0, 1, and 2 for conservative, liberal, and moderate respectively), notice that item 0 is encoded with a 1 in position 0 and 0s elsewhere; item 1 is encoded with a 1 in position 1 and 0s elsewhere; and item 2 is encoded with a 1 in position 2 and 0s elsewhere. So, in general, item i is encoded with a 1 at position i and 0s elsewhere.
Situations where the dependent y-value to predict can take only one of two possible categorical values, such as "male" or "female", can be considered a special case. You can encode such values using standard dummy encoding:
male -> 1 0
female -> 0 1
Alternatively, you can encode using a simple 0-1 encoding like so:
male -> 1
female -> 0
An alternative that is not recommended is to encode non-numeric values along the lines of:
conservative -> 1
liberal -> 2
moderate -> 3
A detailed explanation of why this encoding scheme is usually not a good approach is a bit subtle and is outside the scope of this chapter. But, in short, even though such a scheme works, it usually makes it more difficult for a neural network to learn good weights and bias values.
Encoding non-numeric x-data to numeric values can be done in several ways, but using what is called 1-of-(N-1) effects encoding is usually a good approach. The idea is best explained by example. In the demo, the x-variable home locale can take one of three values: rural, suburban, or urban. To encode N non-numeric values you use N-1 numeric variables like this:
rural -> 1 0
suburban -> 0 1
urban -> -1 -1
As with dummy encoding, the order of the associations is arbitrary. You might have expected to use 1-of-N dummy encoding for x-data. However, for x-data, using 1-of-(N-1) effects encoding is usually much better. Again, the underlying math is a bit subtle.
You might also have expected the encoding for the last item, "urban", to be either (0, 0) or (1, 1) instead of (-1, -1). This is in fact possible; however, using all -1 values for effects encoding the last item in a set typically generates a better neural network prediction model.
Encoding independent x-data which can take only one of two possible categorical values, such as "left-handed" or "right-handed", can be considered a special case of effects encoding. In such situations, you should always encode one value as -1 and the other value as +1. The common computer-science approach of using a 0-1 encoding scheme, though seemingly more natural, is definitely inferior and should not be used.
In summary, to encode categorical independent x-data, use 1-of-(N-1) effects encoding unless the predictor feature is binary, in which case use a -1 and +1 encoding. To encode categorical y-data, use 1-of-N dummy encoding unless the feature to be predicted is binary, in which case you can use either regular 1-of-N dummy encoding, or use 0-1 encoding.
Programmatically encoding categorical data is usually done before any other processing occurs. Programmatically encoding a text file is not entirely trivial. To do so, it is useful to define two helper methods. First, consider helper method EffectsEncoding in Listing 1-b.
static string EffectsEncoding(int index, int N)
{
if (N == 2)
{
if (index == 0) return "-1";
else if (index == 1) return "1";
}
int[] values = new int[N-1];
if (index == N-1) // Last item is all -1s.
{
for (int i = 0; i < values.Length; ++i)
values[i] = -1;
}
else
{
values[index] = 1; // 0 values are already there.
}
string s = values[0].ToString();
for (int i = 1; i < values.Length; ++i)
s += "," + values[i];
return s;
}
Listing 1-b: Helper Method for Effects Encoding
Method EffectsEncoding accepts an index value for a categorical value and the number of possible items the categorical value can take, and returns a string. For example, in the demo program, the x-data locale can take one of three values (rural, suburban, urban). If the input parameters to method EffectsEncoding are 0 (corresponding to rural) and 3 (the number of possible values), then a call to EffectsEncoding (0, 3) returns the string "1,0".
Helper method EffectsEncoding first checks for the special case where the x-data to be encoded can only be one of two possible values. Otherwise, the method creates an integer array corresponding to the result, and then constructs a comma-delimited return string from the array.
Method EffectsEncoding assumes that items are comma-delimited. You may want to pass the delimiting character to the method as an input parameter.
Now consider a second helper method, DummyEncoding, that accepts the index of a dependent y-variable and the total number of categorical values, and returns a string corresponding to dummy encoding. For example, if a y-variable is political inclination with three possible values (conservative, liberal, moderate), then a call to DummyEncoding(2, 3) is a request for the dummy encoding of item 2 (liberal) of 3, and the return string would be "0,0,1".
The DummyEncoding method is defined:
static string DummyEncoding(int index, int N)
{
int[] values = new int[N];
values[index] = 1;
string s = values[0].ToString();
for (int i = 1; i < values.Length; ++i)
s += "," + values[i];
return s;
}
The DummyEncoding method makes the assumption that items are comma-delimited, and skips normal error checking. The method also uses simple string concatenation rather than the more efficient StringBuilder class. The ability to take such shortcuts that can greatly decrease code size and complexity is an advantage of writing your own neural network code from scratch.
Method EncodeFile accepts a path to a text file (which is assumed to be comma-delimited and without a header line), a 0-based column to encode, and a string that can have the value "effects" or "dummy". The method creates an encoded text file. Note that the demo program uses manual encoding rather than calling method EncodeFile.
Suppose a set of raw training data that corresponds to the demo program in Figure 1-c resides in a text file named Politics.txt, and is:
Male,25,Rural,63000.00,Conservative
Female,36,Suburban,55000.00,Liberal
Male,40,Urban,74000.00,Moderate
Female,23,Rural,28000.00,Liberal
A call to EncodeFile("Politics.txt", "PoliticsEncoded.txt", 2, "effects") would generate a new file named PoliticsEncoded.txt with contents:
Male,25,1,0,63000.00,Conservative
Female,36,0,1,55000.00,Liberal
Male,40,-1,-1,74000.00,Moderate
Female,23,1,0,28000.00,Liberal
To encode multiple columns, you could call EncodeFile several times or write a wrapper method to do so. In the demo, the definition of method EncodeFile begins:
static void EncodeFile(string originalFile, string encodedFile,
int column, string encodingType)
{
// encodingType: "effects" or "dummy"
FileStream ifs = new FileStream(originalFile, FileMode.Open);
StreamReader sr = new StreamReader(ifs);
string line = "";
string[] tokens = null;
Instead of the simple but crude approach of passing the encoding type as a string, you might want to consider using an Enumeration type. The code assumes that the namespace System.IO is in scope. Alternatively, you can fully qualify your code. For example, System.IO.FileStream.
Method EncodeFile performs a preliminary scan of the target column in the source text file and creates a dictionary of the distinct items in the column:
Dictionary<string, int> d = new Dictionary<string,int>();
int itemNum = 0;
while ((line = sr.ReadLine()) != null)
{
tokens = line.Split(','); // Assumes items are comma-delimited.
if (d.ContainsKey(tokens[column]) == false)
d.Add(tokens[column], itemNum++);
}
sr.Close();
ifs.Close();
The code assumes there is no header line in the source file. You might want to pass a Boolean parameter named something like hasHeader, and if true, read and save the first line of the source file. The code also assumes the namespace System.Collections.Generic is in scope, and that the file is comma-delimited. There is always a balance between defining a method that is simple but not very robust or general, and using a significant amount of extra code (often roughly twice as many lines or more) to make the method more robust and general.
For the Dictionary object, the key is a string which is an item in the target column—for example, "urban". The value is a 0-based item number—for example, 2. Method EncodeFile continues by setting up the mechanism to write the result text file:
int N = d.Count; // Number of distinct strings.
ifs = new FileStream(originalFile, FileMode.Open);
sr = new StreamReader(ifs);
FileStream ofs = new FileStream(encodedFile, FileMode.Create);
StreamWriter sw = new StreamWriter(ofs);
string s = null; // Result line.
As before, no error checking is performed to keep the main ideas clear. Method EncodeFile traverses the source text file and extracts the strings in the current line:
while ((line = sr.ReadLine()) != null)
{
s = "";
tokens = line.Split(','); // Break apart strings.
The tokens from the current line are scanned. If the current token is not in the target column it is added as-is to the output line, but if the current token is in the target column it is replaced by the appropriate encoding:
for (int i = 0; i < tokens.Length; ++i) // Reconstruct.
{
if (i == column) // Encode this string.
{
int index = d[tokens[i]]; // 0, 1, 2, or . . .
if (encodingType == "effects")
s += EffectsEncoding(index, N) + ",";
else if (encodingType == "dummy")
s += DummyEncoding(index, N) + ",";
}
else
s += tokens[i] +",";
}
Method EncodeFile concludes:
s.Remove(s.Length - 1); // Remove trailing ','.
sw.WriteLine(s); // Write the string to file.
} // while
sw.Close(); ofs.Close();
sr.Close(); ifs.Close();
}
The current result line will have a trailing comma (or whatever delimiting character you specify if you parameterize the method), so the very convenient String.Remove method is used to strip the trailing character away before writing the result line.
Min-Max Normalization
Perhaps the best way to explain min-max normalization is by using a concrete example. In the demo, the age data values are 25, 36, 40, and 23. To compute the min-max normalized value of one of a set of values you need the minimum and maximum values of the set. Here min = 23 and max = 40. The min-max normalized value for the first age, 25, is (25 - 23) / (40 - 23) = 2 / 17 = 0.118. In general, the min-max normalized value for some value x is (x - min) / (max - min)—very simple.
The definition of method MinMaxNormal begins:
static void MinMaxNormal(double[][] data, int column)
{
int j = column;
double min = data[0][j];
double max = data[0][j];
The method accepts a numeric matrix and a 0-based column to normalize. Notice the method returns void; it operates directly on its input parameter matrix and modifies it. An alternative would be to define the method so that it returns a matrix result.
Method MinMaxNormal begins by creating a short alias named j for the parameter named column. This is just for convenience. Local variables min and max are initialized to the first available value (the value in the first row) of the target column.
Next, method MinMaxNormal scans the target column and finds the min and max values there:
for (int i = 0; i < data.Length; ++i)
{
if (data[i][j] < min)
min = data[i][j];
if (data[i][j] > max)
max = data[i][j];
}
Next, MinMaxNormal performs an error check:
double range = max - min;
if (range == 0.0) // ugly
{
for (int i = 0; i < data.Length; ++i)
data[i][j] = 0.5;
return;
}
If both min and max have the same value, then all the values in the target column must be the same. Here, the response to that situation is to arbitrarily normalize all values to 0.5. An alternative is to throw an exception or display a warning message. If all the values of some independent predictor variable are the same, then that variable contains no useful information for prediction.
Notice the demo code makes an explicit equality comparison check between two values that are type double. In practice this is not a problem, but a safer approach is to check for closeness. For example:
if (Math.Abs(range) < 0.00000001)
Method MinMaxNormal concludes by performing the normalization:
for (int i = 0; i < data.Length; ++i)
data[i][j] = (data[i][j] - min) / range;
}
Notice that if the variable range has a value of 0, there would be a divide-by-zero error. However, the earlier error-check eliminates this possibility.
Gaussian Normalization
Gaussian normalization is also called standard score normalization. Gaussian normalization is best explained using an example. The age values in the demo are 25, 36, 40, and 23. The first step is to compute the mean (average) of the values:
mean = (25 + 36 + 40 + 23) / 4 = 124 / 4 = 31.0
The next step is to compute the standard deviation of the values:
stddev = sqrt( ( (25 - 31)2 + (36 - 31)2 + (40 - 31)2 + (23- 31)2 ) / 4 )
= sqrt( (36 + 25 + 81 + 64) / 4 )
= sqrt( 206 / 4 )
= sqrt(51.5)
= 7.176
In words, "take each value, subtract the mean, and square it. Add all those terms, divide by the number of values, and then take the square root."
The Gaussian normalized value for 25 is (25 - 31.0) / 7.176 = -0.84 as shown in Figure 1-c. In general, the Gaussian normalized value for some value x is (x - mean) / stddev.
The definition of method GaussNormal begins:
static void GaussNormal(double[][] data, int column)
{
int j = column; // Convenience.
double sum = 0.0;
for (int i = 0; i < data.Length; ++i)
sum += data[i][j];
double mean = sum / data.Length;
The mean is computed by adding each value in the target column of the data matrix parameter. Notice there is no check to verify that the data matrix is not null. Next, the standard deviation of the values in the target column is computed:
double sumSquares = 0.0;
for (int i = 0; i < data.Length; ++i)
sumSquares += (data[i][j] - mean) * (data[i][j] - mean);
double stdDev = Math.Sqrt(sumSquares / data.Length);
Method GaussNormal computes what is called the population standard deviation because the sum of squares term is divided by the number of values in the target column (in term data.Length). An alternative is to use what is called the sample standard deviation by dividing the sum of squares term by one less than the number of values:
double stdDev = Math.Sqrt(sumSquares / (data.Length - 1));
When performing Gaussian normalization on data for use with neural networks, it does not matter which version of standard deviation you use. Method GaussNormal concludes:
for (int i = 0; i < data.Length; ++i)
data[i][j] = (data[i][j] - mean) / stdDev;
}
A fatal exception will be thrown if the value in variable stdDev is 0, but this cannot happen unless all the values in the target column are equal. You might want to add an error-check for this condition.
Complete Demo Program Source Code
using System;
//using System.IO; // for EncodeFile
//using System.Collections.Generic;
// The demo code violates many normal style conventions to keep the size small.
namespace Normalize
{
class NormalizeProgram
{
static void Main(string[] args)
{
Console.WriteLine("\nBegin data encoding and normalization demo\n");
string[] sourceData = new string[] {
"Sex Age Locale Income Politics",
"==============================================",
"Male 25 Rural 63,000.00 Conservative",
"Female 36 Suburban 55,000.00 Liberal",
"Male 40 Urban 74,000.00 Moderate",
"Female 23 Rural 28,000.00 Liberal" };
Console.WriteLine("Dummy data in raw form:\n");
ShowData(sourceData);
string[] encodedData = new string[] {
"-1 25 1 0 63,000.00 1 0 0",
" 1 36 0 1 55,000.00 0 1 0",
"-1 40 -1 -1 74,000.00 0 0 1",
" 1 23 1 0 28,000.00 0 1 0" };
//Encode("..\\..\\Politics.txt", "..\\..\\PoliticsEncoded.txt", 4, "dummy");
Console.WriteLine("\nData after categorical encoding:\n");
ShowData(encodedData);
Console.WriteLine("\nNumeric data stored in matrix:\n");
double[][] numericData = new double[4][];
numericData[0] = new double[] { -1, 25.0, 1, 0, 63000.00, 1, 0, 0 };
numericData[1] = new double[] { 1, 36.0, 0, 1, 55000.00, 0, 1, 0 };
numericData[2] = new double[] { -1, 40.0, -1, -1, 74000.00, 0, 0, 1 };
numericData[3] = new double[] { 1, 23.0, 1, 0, 28000.00, 0, 1, 0 };
ShowMatrix(numericData, 2);
GaussNormal(numericData, 1);
MinMaxNormal(numericData, 4);
Console.WriteLine("\nMatrix after normalization (Gaussian col. 1" +
" and MinMax col. 4):\n");
ShowMatrix(numericData, 2);
Console.WriteLine("\nEnd data encoding and normalization demo\n");
Console.ReadLine();
} // Main
static void GaussNormal(double[][] data, int column)
{
int j = column; // Convenience.
double sum = 0.0;
for (int i = 0; i < data.Length; ++i)
sum += data[i][j];
double mean = sum / data.Length;
double sumSquares = 0.0;
for (int i = 0; i < data.Length; ++i)
sumSquares += (data[i][j] - mean) * (data[i][j] - mean);
double stdDev = Math.Sqrt(sumSquares / data.Length);
for (int i = 0; i < data.Length; ++i)
data[i][j] = (data[i][j] - mean) / stdDev;
}
static void MinMaxNormal(double[][] data, int column)
{
int j = column;
double min = data[0][j];
double max = data[0][j];
for (int i = 0; i < data.Length; ++i)
{
if (data[i][j] < min)
min = data[i][j];
if (data[i][j] > max)
max = data[i][j];
}
double range = max - min;
if (range == 0.0) // ugly
{
for (int i = 0; i < data.Length; ++i)
data[i][j] = 0.5;
return;
}
for (int i = 0; i < data.Length; ++i)
data[i][j] = (data[i][j] - min) / range;
}
static void ShowMatrix(double[][] matrix, int decimals)
{
for (int i = 0; i < matrix.Length; ++i)
{
for (int j = 0; j < matrix[i].Length; ++j)
{
double v = Math.Abs(matrix[i][j]);
if (matrix[i][j] >= 0.0)
Console.Write(" ");
else
Console.Write("-");
Console.Write(v.ToString("F" + decimals).PadRight(5) + " ");
}
Console.WriteLine("");
}
}
static void ShowData(string[] rawData)
{
for (int i = 0; i < rawData.Length; ++i)
Console.WriteLine(rawData[i]);
Console.WriteLine("");
}
//static void EncodeFile(string originalFile, string encodedFile, int column,
// string encodingType)
//{
// // encodingType: "effects" or "dummy"
// FileStream ifs = new FileStream(originalFile, FileMode.Open);
// StreamReader sr = new StreamReader(ifs);
// string line = "";
// string[] tokens = null;
// // count distinct items in column
// Dictionary<string, int> d = new Dictionary<string,int>();
// int itemNum = 0;
// while ((line = sr.ReadLine()) != null)
// {
// tokens = line.Split(','); // Assumes items are comma-delimited.
// if (d.ContainsKey(tokens[column]) == false)
// d.Add(tokens[column], itemNum++);
// }
// sr.Close();
// ifs.Close();
// // Replace items in the column.
// int N = d.Count; // Number of distinct strings.
// ifs = new FileStream(originalFile, FileMode.Open);
// sr = new StreamReader(ifs);
// FileStream ofs = new FileStream(encodedFile, FileMode.Create);
// StreamWriter sw = new StreamWriter(ofs);
// string s = null; // result string/line
// while ((line = sr.ReadLine()) != null)
// {
// s = "";
// tokens = line.Split(','); // Break apart.
// for (int i = 0; i < tokens.Length; ++i) // Reconstruct.
// {
// if (i == column) // Encode this string.
// {
// int index = d[tokens[i]]; // 0, 1, 2 or . .
// if (encodingType == "effects")
// s += EffectsEncoding(index, N) + ",";
// else if (encodingType == "dummy")
// s += DummyEncoding(index, N) + ",";
// }
// else
// s += tokens[i] +",";
// }
// s.Remove(s.Length - 1); // Remove trailing ','.
// sw.WriteLine(s); // Write the string to file.
// } // while
// sw.Close(); ofs.Close();
// sr.Close(); ifs.Close();
//}
static string EffectsEncoding(int index, int N)
{
// If N = 3 and index = 0 -> 1,0.
// If N = 3 and index = 1 -> 0,1.
// If N = 3 and index = 2 -> -1,-1.
if (N == 2) // Special case.
{
if (index == 0) return "-1";
else if (index == 1) return "1";
}
int[] values = new int[N - 1];
if (index == N - 1) // Last item is all -1s.
{
for (int i = 0; i < values.Length; ++i)
values[i] = -1;
}
else
{
values[index] = 1; // 0 values are already there.
}
string s = values[0].ToString();
for (int i = 1; i < values.Length; ++i)
s += "," + values[i];
return s;
}
static string DummyEncoding(int index, int N)
{
int[] values = new int[N];
values[index] = 1;
string s = values[0].ToString();
for (int i = 1; i < values.Length; ++i)
s += "," + values[i];
return s;
}
} // Program class
} // ns

DISCLAIMER: Web reader is currently in beta. Please report any issues through our support system. PDF and Kindle format files are also available for download.
1. Neural Networks
2. Perceptrons
3. Feed Forward
4. Back Propagation
5. Training
- 1800+ high-performance UI components.
- Includes popular controls such as Grid, Chart, Scheduler, and more.
- 24x5 unlimited support by developers.

